【理科拾遗】2.遗传与卷积

在总结某一类遗传题的时候，我发现它和卷积竟然有着很深的关系。

题目

我所说的「题目」，就是那种经典的叠加效应的题——多对等位基因自由组合，其中显性基因的个数（基因型中大写字母的个数）决定性状（高度/长度等）。

不一定正确的例题

某植物茎的高度由两对等位基因（A，B）控制且遵循自由组合定律。两对等位基因决定茎高度时，显性基因越多其茎高度越高。现已知基因型为AABB的个体茎高度为48cm，基因型为Aabb个体为30cm。则将基因型为AaBb的个体自交，后代中高度为 42cm的个体的比例为？

（我认为的）答案：

这个题目本来很简单——自己画一个经典的4×4基因棋盘然后数一数大写字母的个数就行了。但是在仔细分析这张表之后，发现了一些有趣的东西。

大写个数与杨辉三角

为了方便，让我们还是画一个4×4棋盘，并标注一下每一格的大写字母数量，这张表很重要，接下来叫它表1：

配子	AB	aB	Ab	ab
AB	AABB 4	AaBB 3	AABb 3	AaBb 2
aB	AaBB 3	aaBB 2	AaBb 2	aaBb 1
Ab	AABb 3	AaBb 2	AAbb 2	Aabb 1
ab	AaBb 2	aaBb 1	Aabb 1	aabb 0

接下来统计一下表1中各个数字出现的次数：

大写字母数量	表1中出现的次数
4	1
3	4
2	6
1	4
0	1

那么让我们仔细来分析一下1, 4, 6, 4, 1这个数列。不妨给他起个名字吧。

• 这个数列一定是回文（对称）的。 这是因为，在我们的统计中大写字母和小写字母的地位相等。如果统计小写字母，理论上会得到与统计大写字母相反的结果；又因为地位相等所以会得到和大写字母相同的结果，所以大写字母的统计结果必然是回文的。

• 它是杨辉三角的第4行（从第0行开始）。

除此之外，不仅是两对等位基因，其他数量对等位基因的这个结果也会出现在杨辉三角中。

1. 一对等位基因（Aa 自交）：

2. 三对等位基因（AaBbCc 自交）：

杨辉三角

既然和杨辉三角扯上了关系，那不得不简单看一眼杨辉三角了。

刚刚提到，在本文中，我们在谈论杨辉三角的行数时，总是从0开始数。也就是，1是第0行，1 3 3 1是第3行，以此类推。

由于杨辉三角的性质，这样定义的行数恰好是该行的第二项（除了开头1以外的一项），比如，第4行1 *4* 6 4 1的第二项为4。

深入分析……

首先，让我们看看一个基础而熟悉的表——Aa自交后代的基因棋盘。按照惯例还是写出每个基因型的大写字母个数。这个表叫做表2：

配子	A	a
A	AA 2	Aa 1
a	Aa 1	aa 0

这个表是如此的简单，以至于无需统计——仅凭肉眼即可看出1, 2, 1的数列。

有趣的是，如果我们将表2和表1放在一起对比，则会发现一些有趣的事情。

首先，让我们把表1涂上颜色。

涂色后的表1

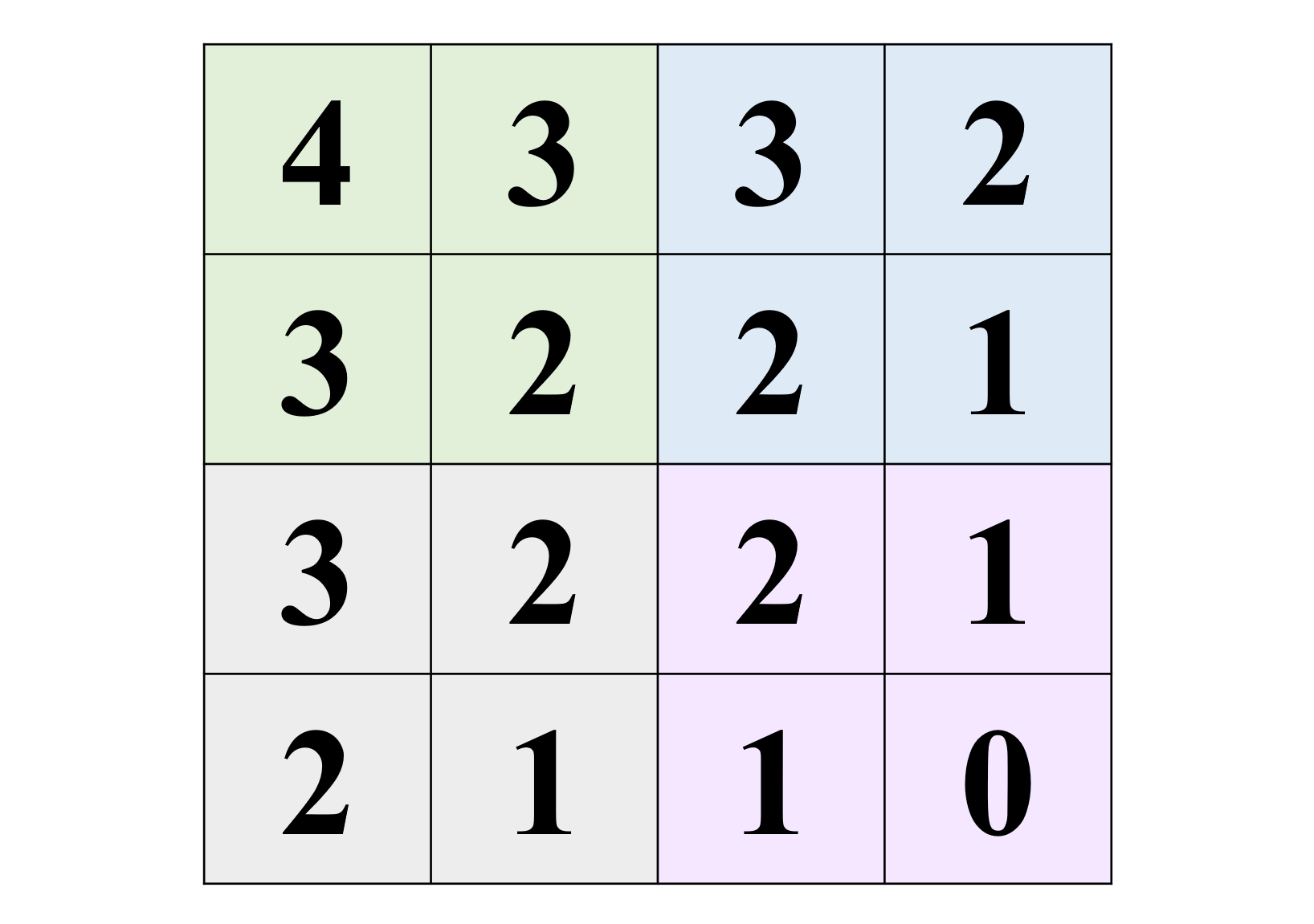
让我们分析一下这张图。

• 看整体。
  • 整个表被分成了四份（不同颜色），注意到左下和右上的内容一样。整体布局类似表2。
  • 从右下色块开始，每个数字+1得到左下和右上色块，+2则得到左上色块。四个色块对应数字差值与表二2-{1,1}-0类似。
• 看局部。
  • 右下色块 与表2一致。
  • 每一个色块内，左下角的数字和右上角的数字相同。并且每一个色块内的差值也类似表二的2-{1,1}-0。

既然整体上和局部上都类似表2，那么显然，我们可以认为，这个表1是表2「嵌套」得来的。具体来讲，就是4个小表2分别嵌入到一个大表2的各个格子中，嵌入时小表2的每个数字加上被嵌入的大表2格子中的数字。

表2嵌套

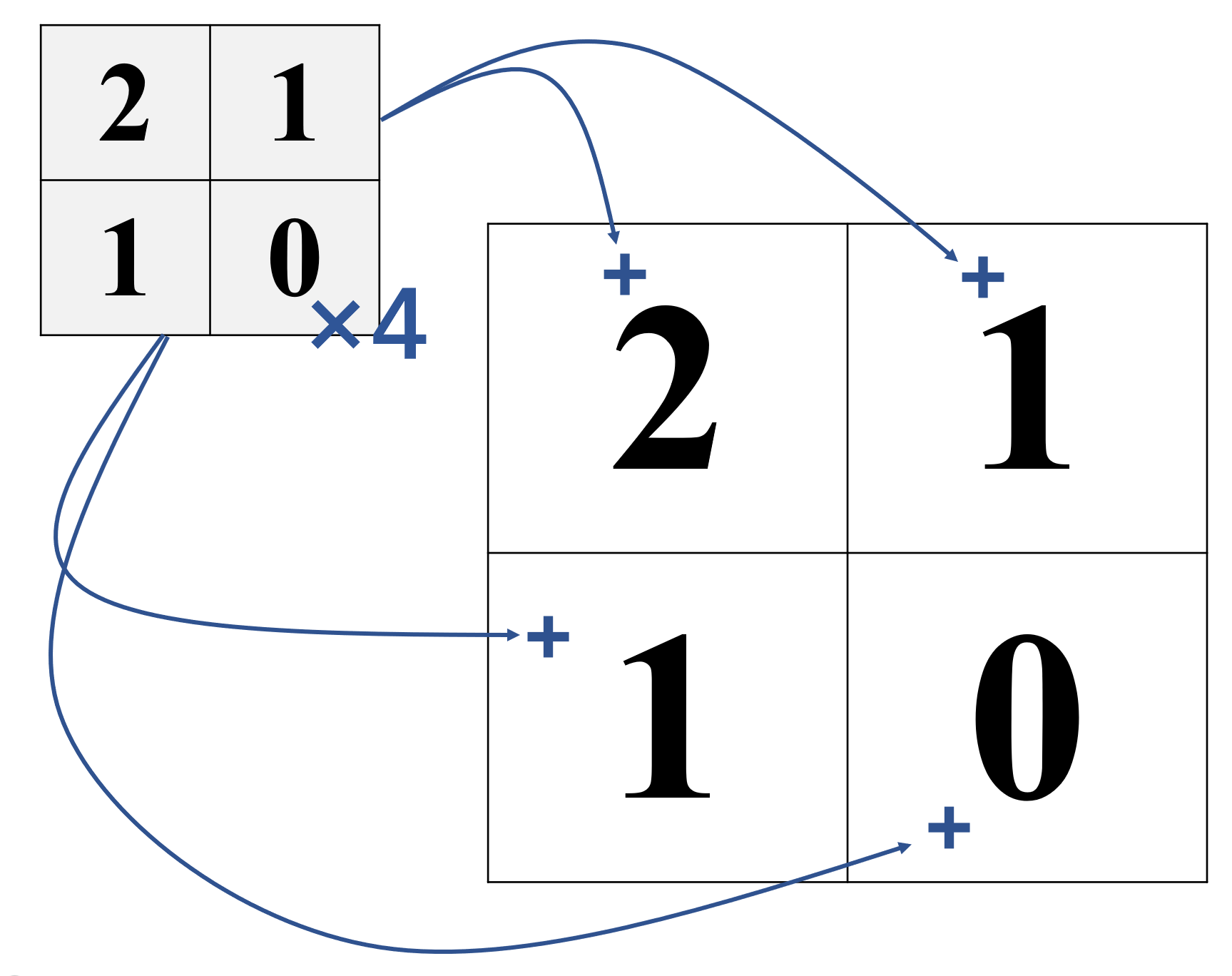
既然表1可以看做是表2此般嵌套后形成的，那表1 1, 4, 6, 4, 1的数列也应该可以看做表2的 1, 2, 1和自身经过某种操作之后形成的。那么究竟是什么操作呢？答案是「卷积」，具体一点，是「离散的」卷积。

卷积

关于卷积，YouTuber、UP主 3Blue1Brown发过一个视频，可以看看：

Bilibili视频

YouTube视频

由于我也讲不清楚，所以在这里我索性也不介绍卷积了。

我们这次只需要了解离散的卷积，而这一点在视频中已经有了体现。所以让我们直接开始尝试吧。

与它自己进行离散卷积之后（「 」是卷积的符号）：

看来我们已经得出了结论。遗传（似乎已经没啥关系了）确实和卷积有关。

深入挖掘……

让我们重新看一眼杨辉三角。

别忘记，本文中对于行的计数是从第0行开始的。

在上一节的例子中， 作为第2行，与它自己（第2行）卷积后得到的 则是第4行。

如果用 表示杨辉三角第n行（）的内容（再次提醒，从0开始），那么刚刚的过程可以表示成：

让我们多试一试，以下是一部分的Python控制台输出：

>>> import numpy as np                #引入卷积函数依赖库
>>> L2=[1,2,1]                        #杨辉三角第二行
>>> L3=[1,3,3,1]                      #第三行
>>> np.convolve(L2, L3)               #计算L2与L3的卷积
array([ 1,  5, 10, 10,  5,  1])
>>> L4=[1,4,6,4,1]                    #第四行
>>> np.convolve(L2, L4)               #计算L2与L4的卷积
array([ 1,  6, 15, 20, 15,  6,  1])
>>> np.convolve(L3, L4)               #计算L3与L4的卷积
array([ 1,  7, 21, 35, 35, 21,  7,  1])

如果你无法理解，上面这段代码显示了几次卷积运算的结果（Python在这里就是个计算器）：

经过了更多的计算，不难发现：

其中 且 表示杨辉三角第n行（从0开始）。

总结

这一次，我们从叠加效应的遗传题出发，着重关注了杂合子自交后代中，基因型大写字母（显性基因）个数的出现次数。然后我们从该次数形成的数列入手，发现其与杨辉三角有很大关系。接着我们分析了它的构造过程，并从中发现其与卷积运算的关系。最后我们还得出了在杨辉三角中的卷积的结论。