【新系列】【理科拾遗】1.导数

在高二正式在数学课本中遇到导数之前，我们和导数已经有了无数的联系……

导数的简介

本节是给那些不了解导数的读者准备的基础概念科普，如果你认为自己已经有相关知识，可以跳过。

导数（英语：derivative）是微积分学中的一个概念。函数在某一点的导数是指这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数 的自变量在一点 上产生一个增量 时，函数输出值的增量与自变量增量 的比值在 趋于0时的极限如果存在，即为 在 处的导数，记作 、 或 。

——来自中文维基百科：导数

似乎这么说，大家都是一头雾水。但是我觉得对于高一的学生来说，我们可以简单地说明一下导数的几何意义：

对于函数，如果它的定义域和值域都是的子集（简单地，自变量和函数值都是实数），那么它在处的导数就是的图像在处的（切线）斜率。

也可以用另外一种易于理解的直观话说：

如果在附近变化得很快，那么它在处的导数的绝对值就越大。

可能有些人看出来了：这不就是位移和速度、速度和加速度嘛！

没错。严格地说，在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。而由一个物体的位移-时间表达式求出它对应的速度-时间表达式的过程，就可以直观地理解为求关于的导函数的过程，简称求导。在这里，便是关于的导函数。

当然，关于一个函数是否有导数还需要进一步地判断（判断一个函数是否可导）。这牵扯到很复杂的概念，在这里不加赘述。只需要读者们牢记求一个函数的导（函）数就相当于求这个函数的变化速度一样。

一些可能用到的求导知识

• 对于，有。 比如的导函数。

• 对于常函数，其导函数为0。即。

在匀变速直线运动中的关联

既然我们直接提到了导数与运动学概念速度的联系，那让我们看看具体的。

在匀速直线运动中，有这两组公式：

如果你想尝试一下，可以试着对关于求导，即求。不出意外，它恰好等于。

推导过程

注意到 则 另外，有 则 故有上述结论。

这个结论似乎并没有出乎我们的意料——导数本该如此。但是当我们了解了一些其他的结论的时候，运动学中的一些结论似乎会变得有意思起来。

二次函数与导数：初中压轴、匀变速、抛体

在初中的二次函数压轴题中，有这样一种常见、简单的题目。比如：

题目Q₁

如图，二次函数的图像经过、，交轴于点。是第一象限内二次函数图像上一点，问当的面积最大时，点的坐标。

在初中，大家都用的是「铅锤高 水平宽」的方法，用点坐标表达的面积，再研究这个表达式的最值得出结果。

但是有了导数这个强大的工具，我们得以降维打击，秒杀这一道题。

解：计算（过程略）可得到二次函数解析式

且，则直线AB的斜率

分析得当抛物线过点的切线平行于直线时，的面积取到最大值。对求导得

设此时点坐标为，则

将代入得此时P点坐标为

和之前一样，这个过程中没有在求导前判断函数可导，不够严谨。并且这种方法在初中还不一定能得到分，充其量作为一种辅助检测答案的方法。

一个有趣的引理

如果每次都是像上面那样，求导、联立，虽然帅，但是不够快。于是就有了这一节，分享一个引理，并探讨一下它能推导出什么。

拉格朗日中值定理

首先我们先简单介绍一下拉格朗日中值定理，它的表述是：

如果函数满足：

• 在闭区间上连续;

• 在开区间内可微分;

那么至少有一点 ，使下面等式成立

——来自中文维基百科：拉格朗日中值定理

上面的等式也可以写成

不难发现，写成分式之后，等号右边就是过的图像上两点的直线的斜率，也就是在上的平均变化率。

也许有些读者还是没有理解拉格朗日定理的意义，所以让我们给出它的几何意义：

几何意义

若连续曲线在点之间的每一点处都有不垂直于轴的切线，则曲线在、间至少存在一点，使得该点处的切线与割线平行。

——来自百度百科：拉格朗日中值定理§定理推广

有了这些知识（其实没有问题也不大），我们可以开始讲述我们的引理了。

引理L₁

对于形如的二次函数上的区间，有

希望读者们看这么一点就能立刻明白是怎么一回事。谨防万一我在这里还是给出它的几何意义。

几何意义

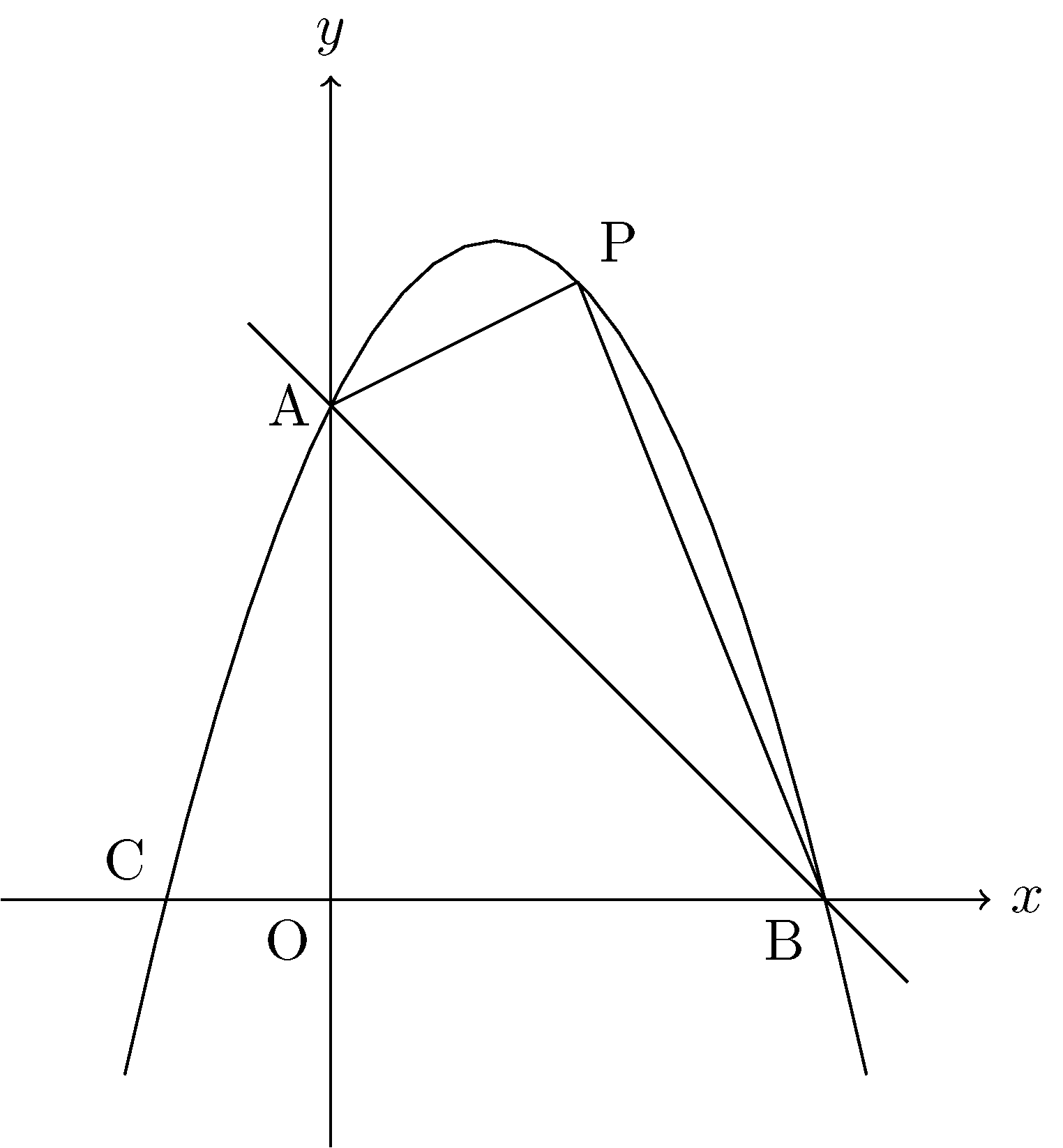
对于任意的一条抛物线和过其上两点的割线，抛物线过的切线平行于。

证明

对于等式的右边，将其展开：

在上连续可导，根据拉格朗日中值定理 则 可得

引理的应用

二次函数压轴

有了引理，刚刚的例题Q₁便可以被真正「秒杀」：

解：计算可得到二次函数解析式

且

分析得当抛物线过点的切线平行于直线时，的面积取到最大值。

根据引理，可知当点横坐标满足

时的面积最大。

此时点坐标为